Little Space for Things of Little Importance - Tinkering with Compression
I was watching this video from Numberphile where Zoe Griffiths tries to memorize the sequence of Red and Black cards. And I was thinking, “this is a good example to explain how compression works”.
A compression algorithm can either be a lossless or a lossy algorithm. A compression algorithm is considered lossless when there is no information reduction after compressing; these kind of algorithms work by reducing statistical redundancy, e.g. by back-referencing repeated portions of the data. The ZIP format implements lossless compression. On the other hand, the lossy algorithms remove unnecessary data or noise from the original representation. The decompressed representation obtained after reversing a lossy compression is only an approximation of the original representation. MP3 uses lossy data compression
What I’m implementing here is a form of lossless compression called Run-Length Encoding (RLE), and it will be used to store the sequence of Red and Black cards in a deck of cards. You can find the source code here.
First, some boilerplate
I can’t do deck compression without having a deck first. So, let there be Card:
1
2
3
4
5
6
7
8
9
10
11
12
13
package cardistry
const (
Spades string = "♠️"
Hearts = "♥️"
Diamonds = "♦️"
Clubs = "♣️"
)
type Card struct {
Number int32
Suit string
}
For simplicity when dealing with card colors, I added two boolean Red() and Black() methods to Card, as well as a Color() method.
I also want a way to create a shuffled deck of cards, so here it goes:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
package cardistry
type Deck []Card
func NewDeck() *Deck {
d := &Deck{}
suits := []string{Spades, Hearts, Diamonds, Clubs}
for _, suit := range suits {
for i := 1; i <= 13; i++ {
*d = append(*d, Card{Number: uint32(i), Suit: suit})
}
}
return d
}
func (d *Deck) Shuffle() {
rand.Seed(time.Now().UnixNano())
// Fisher Yates shuffle
rand.Shuffle(len(*d), func(i, j int) {
(*d)[i], (*d)[j] = (*d)[j], (*d)[i]
})
}
Compression of said deck
Since I only care about the color of the cards, one way to compress them is to keep a tally of how many cards of the same color are in a sequence, and store the sequences lengths (tallies) in an array. I also need to know the color of the first card. E.g., for the following deck:
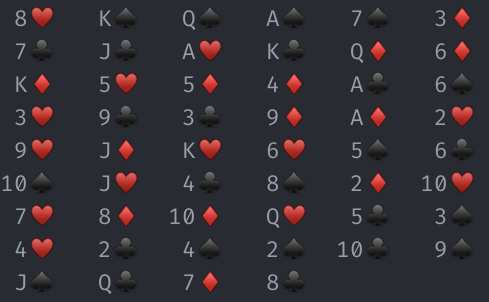
I only need need to store the starting color (Red) as well as the tallies:
1
[1 4 1 2 1 1 6 2 1 2 7 3 1 2 6 2 1 7 1 1]
To “compress” the deck of cards into a first color and an array of sequences:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// Compress the deck
// @return sign: false means the series starts with Black,
// true means it starts with Red
// @return sequences: lengs of the sequences of the same color
func (d *Deck) Compress() (bool, []uint32) {
sign := false
firstCard := (*d)[0]
if firstCard.Red() {
sign = true
}
// count them
var sequences []uint32
prevIndex := 0
for index, card := range *d {
if index == 0 { // First count, nothing to compare with
sequences = append(sequences, 1)
continue
}
// Compare with previous card
prevCard := (*d)[index-1]
// If the color is the same, increment the count
if card.Color() == prevCard.Color() {
sequences[prevIndex] += 1
continue
}
// add a new count
sequences = append(sequences, 1)
prevIndex += 1
}
return sign, sequences
}
In this implementation, the sequences array is storing int32 for each tally, so 4 bytes per each count. That’s too much!
The maximum number of cards of the same color that can be in a sequence is 26 (e.g. if all the Spades and all the Clubs are in the same sequence). I don’t need more than 5 bits to store the number 26 so using int32 for these is an overkill; I’m wasting precious bits that I could be using to store more valuable data. So, instead of using 4 bytes to store each tally, I’m going to do some bitwise magic and store multiple, different tallies in the same int32.
Since all sequence lengths are not wider than 5 bits, I can store up to 6 of them in the same int32, like this:
The 2 Most Significant Bits I am not using (yet), and the rest of the bits of the int32 are storing the sequence lengths, sort of multiplexed (for lack of a better word):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
package cardistry
type ColorSeq struct {
Sign bool
Frame []uint32
}
// Creates new ColorSeq from a deck
// @param sign: the sign of the deck
// @param arr: array of sequence lengths
// @return ColorSeq: the compressed sequence
func NewColorSeq(sign bool, arr []int32) *ColorSeq {
frame := make([]uint32, len(arr)/6+1)
robin := 0
frameIdx := 0
bigboi := uint32(0)
for _, num := range arr {
bigboi = bigboi | uint32(num)<<(robin*5)
robin++
if robin == 6 { // reset robin and bigboi
frame[frameIdx] = bigboi
robin = 0
bigboi = 0
frameIdx++
}
frame[frameIdx] = bigboi
}
return &ColorSeq{Sign: sign, Frame: frame}
}
// Convert from a ColorSeq to a sign and a tally
func (cs *ColorSeq) Decompress() string {
var s string
if cs.Sign {
s += "R "
} else {
s += "B "
}
for _, num := range cs.Frame {
// num needs to be and'd with 0x1F to get the last 5 bits
for i := 0; i < 6; i++ {
s += strconv.Itoa(int(num&0x1F)) + " "
num = num >> 5
}
}
return s
}
You can see the bitwise wizardry in action here. In the NewColorSeq() method I’m using a variable called robin to sorta “round-robin”-ify in which position (Seq1 through Seq6) should the color sequence be put. I’m also using a bigboi variable to accumulate these Seq1 through Seq6 values into a single int32.
When Decompressing, which is the opposite of compressing tallies into a single int32, I’m AND-ing the “bigboi” int32 with 0x1F (11111 in binary) and shifting it 5 bits to the right, so I can continue getting the values Seq1 through Seq6.
Putting it all together:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
package main
import (
"aziflaj/cardcompress/cardistry"
"fmt"
)
func main() {
deck := cardistry.NewDeck()
deck.Shuffle()
fmt.Println(deck)
sign, tally := deck.Compress()
fmt.Println(tally)
matrix := cardistry.NewColorSeq(sign, tally)
fmt.Println(matrix)
fmt.Println(matrix.Decompress())
}
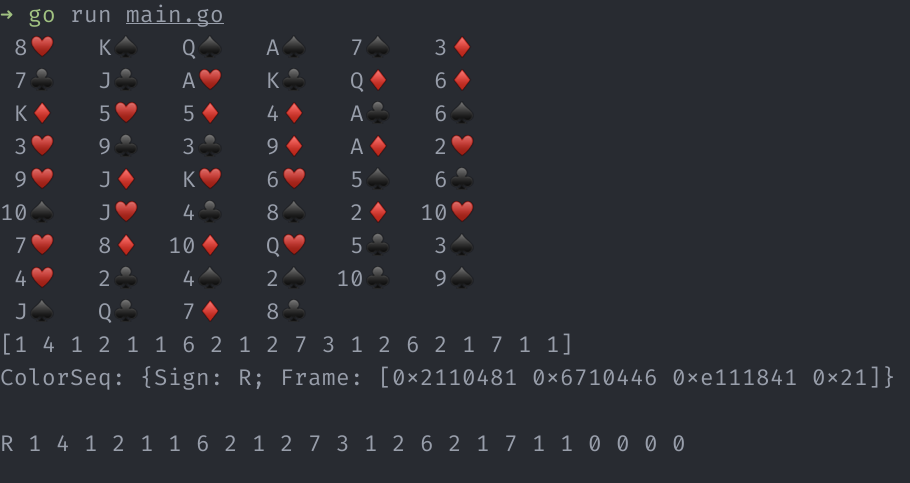
And a sample output:
What about sizes?
I don’t know yet if this cOmPrEsSiOn AlGoRiThM actually does any good. So I’m dumping everything in files and see if there’s some difference in file size before and after applying this compression. Specifically, I want to compare the file size of 3 binary files:
- The file of int32 tallies
- The file of int32 ColorSeq Frames
- The file of uint8 tallies
So, to update the code, I added a writeToFile function to simplify dumping arrays into a binary file:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func writeToFile(filename string, data any) error {
file, err := os.Create(filename)
if err != nil {
return err
}
defer file.Close()
buf := new(bytes.Buffer)
err = binary.Write(file, binary.LittleEndian, data)
if err != nil {
return err
}
file.Write(buf.Bytes())
return nil
}
func main() {
// ...
sign, tally := deck.Compress()
err := writeToFile("tally.bin", tally)
matrix := cardistry.NewColorSeq(sign, tally)
err = writeToFile("matrix.bin", matrix.Frame)
// ...
}
Then, to see the difference in file size:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
➜ go run main.go; ls -h -l tally.bin matrix.bin
8♥️ K♠️ Q♠️ A♠️ 7♠️ 3♦️
7♣️ J♣️ A♥️ K♣️ Q♦️ 6♦️
K♦️ 5♥️ 5♦️ 4♦️ A♣️ 6♠️
3♥️ 9♣️ 3♣️ 9♦️ A♦️ 2♥️
9♥️ J♦️ K♥️ 6♥️ 5♠️ 6♣️
10♠️ J♥️ 4♣️ 8♠️ 2♦️ 10♥️
7♥️ 8♦️ 10♦️ Q♥️ 5♣️ 3♠️
4♥️ 2♣️ 4♠️ 2♠️ 10♣️ 9♠️
J♠️ Q♣️ 7♦️ 8♣️
[1 4 1 2 1 1 6 2 1 2 7 3 1 2 6 2 1 7 1 1]
ColorSeq: {Sign: R; Frame: [0x2110481 0x6710446 0xe111841 0x21]}
R 1 4 1 2 1 1 6 2 1 2 7 3 1 2 6 2 1 7 1 1 0 0 0 0
-rw-r--r-- 1 aldo staff 16B Jan 29 22:15 matrix.bin
-rw-r--r-- 1 aldo staff 80B Jan 29 22:15 tally.bin
The compressed matrix.bin file is taking 16Bytes, as opposed to 80Bytes that are required to store the array of sequence lengths. If I also compare hexdumps between the binary files, I get the following:
1
2
3
4
5
6
7
8
9
10
11
➜ hexdump -C tally.bin
00000000 01 00 00 00 04 00 00 00 01 00 00 00 02 00 00 00 |................|
00000010 01 00 00 00 01 00 00 00 06 00 00 00 02 00 00 00 |................|
00000020 01 00 00 00 02 00 00 00 07 00 00 00 03 00 00 00 |................|
00000030 01 00 00 00 02 00 00 00 06 00 00 00 02 00 00 00 |................|
00000040 01 00 00 00 07 00 00 00 01 00 00 00 01 00 00 00 |................|
00000050
➜ hexdump -C matrix.bin
00000000 81 04 11 02 46 04 71 06 41 18 11 0e 21 00 00 00 |....F.q.A...!...|
00000010
It’s a bit more difficult to understand what’s in the matrix.bin file, given the values are multiplexed into bytes, but it’s quite easy to read tally.bin. The first 01 00 00 00 is the same 1 that shows up in the beginning of the sequence; the 1 that means “One red card” in the beginning of the sequence, and it’s written as 01 00 00 00 instead of 00 00 00 01 because of the little endian-ness.
Now, to see how much of a difference it would make if instead of using int32 for Card faces, I’d use uint8:
1
2
3
4
5
type Card struct {
- Number int32
+ Number uint8
Suit string
}
After updating all the places where this uint8 is now used, I get the following file sizes from the same program:
1
2
-rw-r--r-- 1 aldo staff 16B Jan 29 22:26 matrix.bin
-rw-r--r-- 1 aldo staff 20B Jan 29 22:26 tally.bin
and hexdumped:
1
2
3
4
5
6
7
8
➜ hexdump -C matrix.bin
00000000 81 04 11 02 46 04 71 06 41 18 11 0e 21 00 00 00 |....F.q.A...!...|
00000010
➜ hexdump -C tally.bin
00000000 01 04 01 02 01 01 06 02 01 02 07 03 01 02 06 02 |................|
00000010 01 07 01 01 |....|
00000014
Compared to the hexdump from above, uint8 requires less bytes that int32, but it’s still more than the “very compressed” compressed approach.
Run-Length Encoding is a simple and naive approach to compression. It was initially used during the late 60s in analog TV transmissions and fax machines. Even though mostly replaced with newer, better compression techniques, RLE still finds usage in DEFLATE, the algorithm behind the ZIP file format, as well as in PDF and GIF file formats.